I recently started studying nano-chemistry. To be more precise, exactly one year ago! Naturally, this requires knowledge in “normal” chemistry. Back in high school chemistry was… mysterious. But now, equipped with some university physics, linear algebra and quantum mechanics, chemistry looks different. So, with a fresh restart in the area, starting with stoichiometric calculations (that is, balancing equations of reaction), some ideas already come to mind, and I started to investigate a property that I call “stoichiometric degeneracy”. I have been writing this post over the past year, and I have been adding material to it as my knowledge in the subject has increased. Now I just picked up a book on chemical kinetics and I realize that I could keep on appending to this article for another year… But the main idea is there, and just like with peacocks you sometimes just gotta let it fly!

Contents

Introduction

The first example pulled up in a lecture was a combustion reaction of ethane

$$ \underbrace{C_2 H_6}_{\text{Ethane}} + \underbrace{O_2}_{\text{Oxygen}} \rightarrow \underbrace{CO_2}_{\text{Carbon dioxide}} + \underbrace{H_2 O}_{\text{Water}} $$

The stoichiometric task is to determine coefficients $X = (X_1, X_2, X_3, X_4)$ such that

$$ {\color{orange} X_1} C_2 H_6 + {\color{orange} X_2} O_2 \rightarrow {\color{orange} X_3} CO_2 + {\color{orange} X_4} H_2 O $$

Let us define an atomic basis as a sequence of unique atoms in the reaction: $(C, H, O)$. Using this basis, we assign a molecule a coordinate by counting the number of atoms of each type in the basis

$$ {\color{orange} X_1} \underbrace{C_2 H_6}_{(2, 6, 0)} + {\color{orange} X_2} \underbrace{O_2}_{(0, 0, 2)} \rightarrow {\color{orange} X_3} \underbrace{CO_2}_{(1, 0, 2)} + {\color{orange} X_4} \underbrace{H_2 O}_{(0, 2, 1)} $$

The stoichiometric equation can now be rewritten in matrix form as

$$\begin{pmatrix} 2 & 0 \newline 6 & 0 \newline 0 & 2 \end{pmatrix} \begin{pmatrix} X_1 \newline X_2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \newline 0 & 2 \newline 2 & 1 \end{pmatrix} \begin{pmatrix} X_3 \newline X_4 \end{pmatrix}$$

performing the matrix vector multiplication gives a set of equations

$$\begin{pmatrix} 2 X_1 \newline 6 X_1 \newline 2 X_2 \end{pmatrix} = \begin{pmatrix} X_3 \newline 2 X_4 \newline 2 X_3 + X_4 \end{pmatrix}$$

which is easy to solve by hand

$$\begin{eqnarray} X_3 &=& 2 X_1 \newline 2 X_4 &=& 6 X_1 \Rightarrow X_4 = 3 X_1 \newline 2 X_2 &=& 2 X_3 + X_4 = 4 X_1 + 3 X_1 = 7 X_1 \Rightarrow X_2 = \frac{7}{2} X_1 \end{eqnarray}$$

Since only integer values coefficients are permissible, we set $X_1 = 2$ to get the solution

$$ {\color{orange} 2} C_2 H_6 + {\color{orange} 7} O_2 \rightarrow {\color{orange} 4} CO_2 + {\color{orange} 6} H_2 O $$

This reaction is simple enough to make the system of equations easy to solve manually. For a general reaction with $M$ reactants and $N$ products involving molecules consisting of $K$ unique type of atoms, we can describe it in matrix form as $A x = B y$ where $A$ and $B$ are molecular coordinate matrices created by stacking the molecular coordinates of each participant in the reaction horizontally (with shapes ${K \times M}$ and $K \times N$ respectively), and $x$ and $y$ are the vectors with unknown stoichiometric coefficients. Define the stoichiometric coefficient vector $z$ as the concatenation $(x,y)$ of the reactant and product coefficients, and define the stoichiometric coordinate matrix $C$ as the horizontal concatenation $(A, -B)$. With these definitions in mind, any stoichiometric equation can then be formulated as a null space finding problem $C z = 0$. For the example above, the coordinate matrix is

$$\begin{pmatrix} 2 & 0 & -1 & 0 \newline 6 & 0 & 0 & -2 \newline 0 & 2 & -2 & -1 \end{pmatrix}$$

It is easy to verify that the matrix rank is 3, hence the null space is one-dimensional and only a single solution (up to scale) exists. One can also quickly check that the solution $(2,7,4,6)$ found earlier is indeed a null vector (and hence a solution) as it should be. The solution is also minimal (that is, they can not be reduced to smaller numbers) since the coefficients are coprime.

Stoichiometric degeneracy

A question naturally arises: are reactions guaranteed to have a one-dimensional null space or could there be linearly independent solutions giving different reactant/product stoichiometric coefficients? If such a reaction exist, then the number of reactants and products must exceed the number of distinct atoms by at least two. Scrolling through examples on the internet, almost all educational examples have exactly one more compound than the number of distinct atoms! Eventually I encountered this equation for gun powder combustion 1

$$ \underbrace{10 KNO_3}_{\text{Potassium nitrate (Saltpeter)}} + 3 S + 8 C \rightarrow \underbrace{2 K_2 CO_3}_{\text{Potassium carbonate (salt)}} + \underbrace{3 K_2 SO_4}_{\text{Potassium sulfate (salt)}} + 6 C O_2 + 5 N_2 $$

This reaction incorporates 5 different atoms, but have 3 reactants and 4 products, so there might actually be other solutions than the “official solution” above. Let us forget the coefficients above and write the equation in terms of the atomic basis $(C, K, N, O, S)$

$$ \underbrace{KNO_3}_{(0,1,1,3,0)} + \underbrace{S}_{(0,0,0,0,1)} + \underbrace{C}_{(1,0,0,0,0)} \rightarrow \underbrace{K_2 CO_3}_{(1,2,0,3,0)} + \underbrace{K_2 SO_4}_{(0,2,0,4,1)} + \underbrace{C O_2}_{(1,0,0,2,0)} + \underbrace{N_2}_{(0,0,2,0,0)} $$

and then find the null space of the corresponding stoichiometric coordinate matrix

$$\begin{pmatrix} 0 & 0 & 1 & -1 & 0 & -1 & 0 \newline 1 & 0 & 0 & -2 & -2 & 0 & 0 \newline 1 & 0 & 0 & 0 & 0 & 0 & -2 \newline 3 & 0 & 0 & -3 & -4 & -2 & 0 \newline 0 & 1 & 0 & 0 & -1 & 0 & 0 \end{pmatrix}$$

Using the SymPy 2 software package gives me these solutions (see appendix for script)

$$\begin{eqnarray} % https://tex.stackexchange.com/questions/452677/how-to-align-negative-and-positive-values-inside-an-align-environment \newcommand{\nm}{\mathbin{\phantom{-}}} \newcommand\vec[1]{\boldsymbol #1} \vec{X} &=& (0 , -2 , \nm 3 , \nm 2 , -2, \nm 1, \nm 0) \newline \vec{Y} &=& (2 , \nm 3 , - 2 , -2 , \nm 3, \nm 0, \nm 1) \end{eqnarray}$$

which are obviously not valid by themselves since they have negative coefficients. Only certain linear combinations of these actually constitute a real solution. One such solution is

$$ \vec{X} + \vec{Y} = (2,1,1,0,1,1,1) $$

which actually is a different reaction from the one I found initially altogether (missing $K_2NO_3$ product)!

$$ 2 KNO_3 + S + C \rightarrow K_2 SO_4 + C O_2 + N_2 $$

This reaction looks simpler than the initial gun powder reaction. Question is, when is this preferred over the other? Stoichiometry alone fail to explain this, and there must be some physics involved that determine this…

Let us continue to investigate more solutions. An interesting aspect of solving the stoichiometric equations is that physics impose integer constrained solutions. In general, the null vectors may have coefficients in the rational field $\mathbb{Q}$ as in the first example (where we had $X_2 = \frac{7}{2}X_1$), and we can generate solutions by taking linear combinations of these with coefficients in $\mathbb{Q}$ as well. So, the solution generation problem can be formulated as follows:

Given vectors $x_1, x_2, …, x_M \in \mathbb{Q}^N$ spanning the null space of $C$, find all solutions on the form $p = q_1 x_1 + q_2 x_2 + … + q_M x_M$ with $q_1, …, q_m \in \mathbb{Q}$ such that $p \in \mathbb{Z}_+^{N}$. This can be formulated as a matrix problem by stacking $x_1, …, x_m$ vertically into a matrix $X$, and form the column vector $q = (q_1, …, q_M)^T$ of reaction coefficients, such that $p = Xq$. If the coefficients of $p$ have a common factor, the solution can be rescaled into canonical form by dividing with the largest common divisor.

Ok now it got a bit theoretical, let’s get back to the gun powder reaction and find all solutions to the equation $aX + bY \in \mathbb{Z}_+^N ; a, b \in \mathbb{Q}$. This corresponds to setting $q_1 = a$, $q_2 = b$, $x_1 = X$ and $x_2 = Y$ in the general form above. Writing out each element of the vector and rearranging a bit gives the following set of equations

$$ \newcommand\Nats{\mathbb{Z}_+} aX + bY = a \begin{pmatrix}0 \newline -2 \newline 3 \newline 2 \newline -2 \newline 1 \newline 0 \end{pmatrix} + b \begin{pmatrix}2 \newline 3 \newline -2 \newline -2 \newline 3 \newline 0 \newline 1 \end{pmatrix} = \begin{eqnarray} 2 b \in \Nats \newline 3 b - 2 a \in \Nats \newline 3 a - 2 b \in \Nats \newline 2 a - 2 b \in \Nats\newline 3 b - 2 a \in \Nats\newline a \in \Nats \newline b \in \Nats \end{eqnarray} $$

which is equivalent to (rearranged in order of importance)

$$ \begin{eqnarray} a, b \in \Nats \newline 3 b - 2 a \in \Nats \newline 2 a - 2 b \in \Nats \newline 3 a - 2 b \in \Nats \newline \end{eqnarray} $$

which can be simplified to

$$\begin{eqnarray} a, b &\in& \Nats \newline a &\geq& b \newline 2 a &\leq& 3 b \newline \end{eqnarray}$$

This gives a way to generate all possible solutions to the reaction! The trivial solution $a = b = 0$ is obviously uninteresting. For every $b \geq 1$, enumerate all $a \geq b \in \Nats$ such that $2 a \leq 3 b$. If $a$ and $b$ have a common factor, then skip (since the solution must have been generated earlier). Below is a table for the first few reaction coefficients $a$ and $b$ and the corresponding stoichiometric coefficients

b a $K NO_3$ $S$ $C$ $K_2 C O_3$ $K_2 S O_4$ $C O_2$ $N_2$
1 1 2 1 1 0 1 1 1
2 3 4 0 5 2 0 3 2
3 4 6 1 6 2 1 4 3
4 5 8 2 7 2 2 5 4
5 6 10 3 8 2 3 6 5
5 7 10 1 11 4 1 7 5

The table goes on forever. The first solution we have already analyzed and established that it is missing potassium carbonate as a product. The second solution is interesting as well, but this reaction is missing sulfur as a reactant, and hence potassium sulfate as a product. Since this solution removes a reactant it can be considered uninteresting from a chemical point of view, unless that reactant is a limiting agent forcing a transition to some other reaction state with different reaction coefficients. The third solution is the first that contain all reactants and products. The fifth solution can be identified as the official solution provided by reference. What makes this particular solution special? Are certain solutions non-physical and just a mathematical mirage?

Perhaps a real reaction involves a superposition of all possible reaction states, weighted by their probability to occur? I am wearing my statistical physics hat now, and imagine that the probability of certain reaction states to occur depends on thermodynamic variables such as temperature, pressure, and chemical quantities such as molecular binding energy and how well mixed the reactants are. One could then expect that the reaction states with smaller solution coordinates to be more likely to occur than those with higher coordinates, since they include fewer molecular interactions and should be in some sense be more probable to happen. I believe that this would induce something like a Boltzmann distribution over reaction states. Measuring the ratios of products on a macroscopic scale would then be equivalent to taking the expected value over all reaction states, which happen on the micro scale. The average value might yield arbitrary coefficients, but rounding off to nearest integers could make the solution $(a,b) = (6,5)$ a good approximation. Performing the experiment under other thermodynamic conditions could give different coefficients and make that solution a worse approximation. Could it be, as in quantum mechanics, that there is a difference between the “expected reaction state” and the “most likely reaction state”, so that even though solution $(a,b) = (4,3)$ is more likely, the average is often closer to $(a,b) = (6,5)$?

Let us dive deeper and investigate these questions in more detail. Will you take the red pill and jump down the rabbit hole together with me, or do will you take the blue and chicken out?

Reaction mechanisms

I see you took the red pill, good choice.

In order to theoretically approach this, we need to analyze the reaction paths that can be taken. Think closer about it, what is the chance of 10 molecules of saltpeter, 3 sulfur atoms and 8 coal atoms to come together and react simultaneously? It must be very unlikely! This is the insight that leads to the classical kinetic equations of reaction in solution chemistry (also known as the law of mass action). Given a reaction $aA + bB \rightarrow cC$, assuming a dilute system the rate of reaction is related to the concentrations $[A]$ and $[B]$ through a power law $[A]^{a^\prime} [B]^{b^\prime}$, where $a^\prime \leq a$ and $b^\prime \leq b$. For simple reactions that can not be broken down into elementary reaction steps, the rate exponents $a = a^\prime$ and $b = b^\prime$ coincide with the stoichiometric coefficients. The rate law is easy to understand, just look at small area of space and do a probability calculation of the chemical species coming together; since the system is assumed to be dilute, higher order terms can be equated to zero. Let us start by breaking down the holistic gun powder reaction without stoichiometric coefficients, with the physical phases annotated

$$ KNO_3(s) + S(s) + C(s) \rightarrow K_2 CO_3(s) + K_2 SO_4(s) + CO_2(g) + N_2(g) $$

into (almost) all possible (reversible) elementary combination/decomposition reactions. There exist a combinatorial amount of ways to artificially decompose this reaction. A molecule of N atoms can be decomposed into $B_N = \sum_{k=0}^N { N \choose k } B_k$ partitions, where $B_N$ is called the N:th Bell number. That gives $B_5 = 52$ ways to decompose $KNO_3$ into smaller molecules. You can see how this quickly become a problem, most suitable for a computer to solve for us. For illustrational purposes, let us pick some well informed choices of decomposition. For example, the decomposition $KN + O_3$ does not help us that much, because $KN$ is not a stable compound for which we have any data for. This could have been realized by simply looking at it’s molecular structure

image/svg+xml O N O O K
Figure 1: Molecular structure of potassium nitrate, showing the character of each bond in the molecule.

$KNO_3$ is a salt and hence stick together through an ionic bond between a $K^+$ potassium cation and a $NO_3^-$ nitrate anion. It seems unlikely then, that any decomposition other than that breaking the ionic bond ($KNO_3 \rightleftharpoons K^+ + NO_3^-$) will occur during reaction. A further complication arise from the fact that $KNO_3$ atoms does not exist in isolation but crystallize in the patterns shown below.

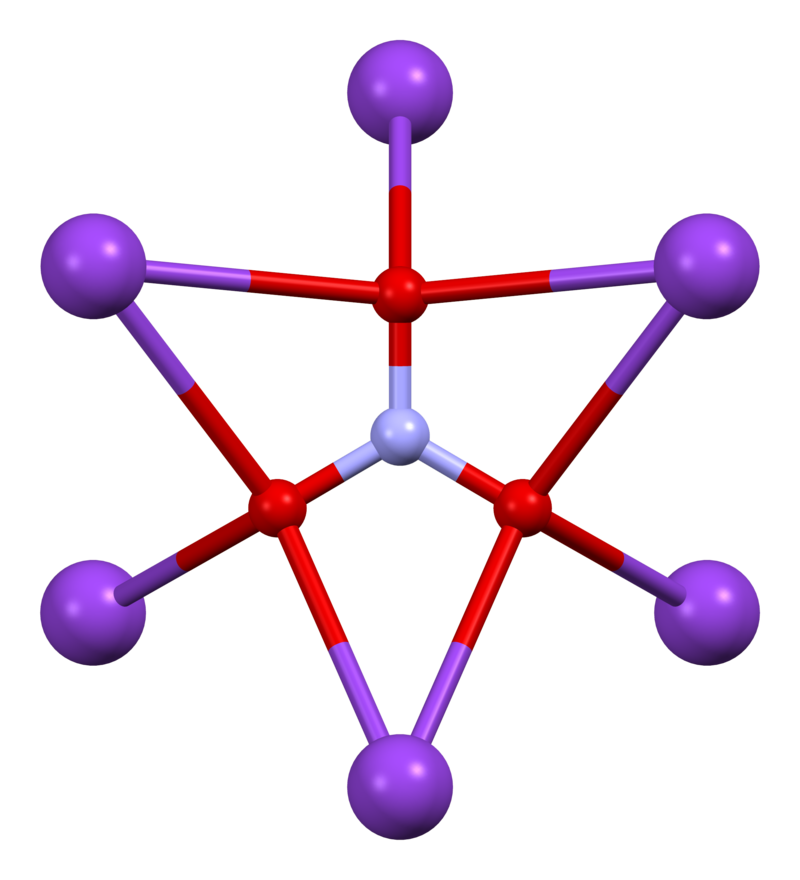
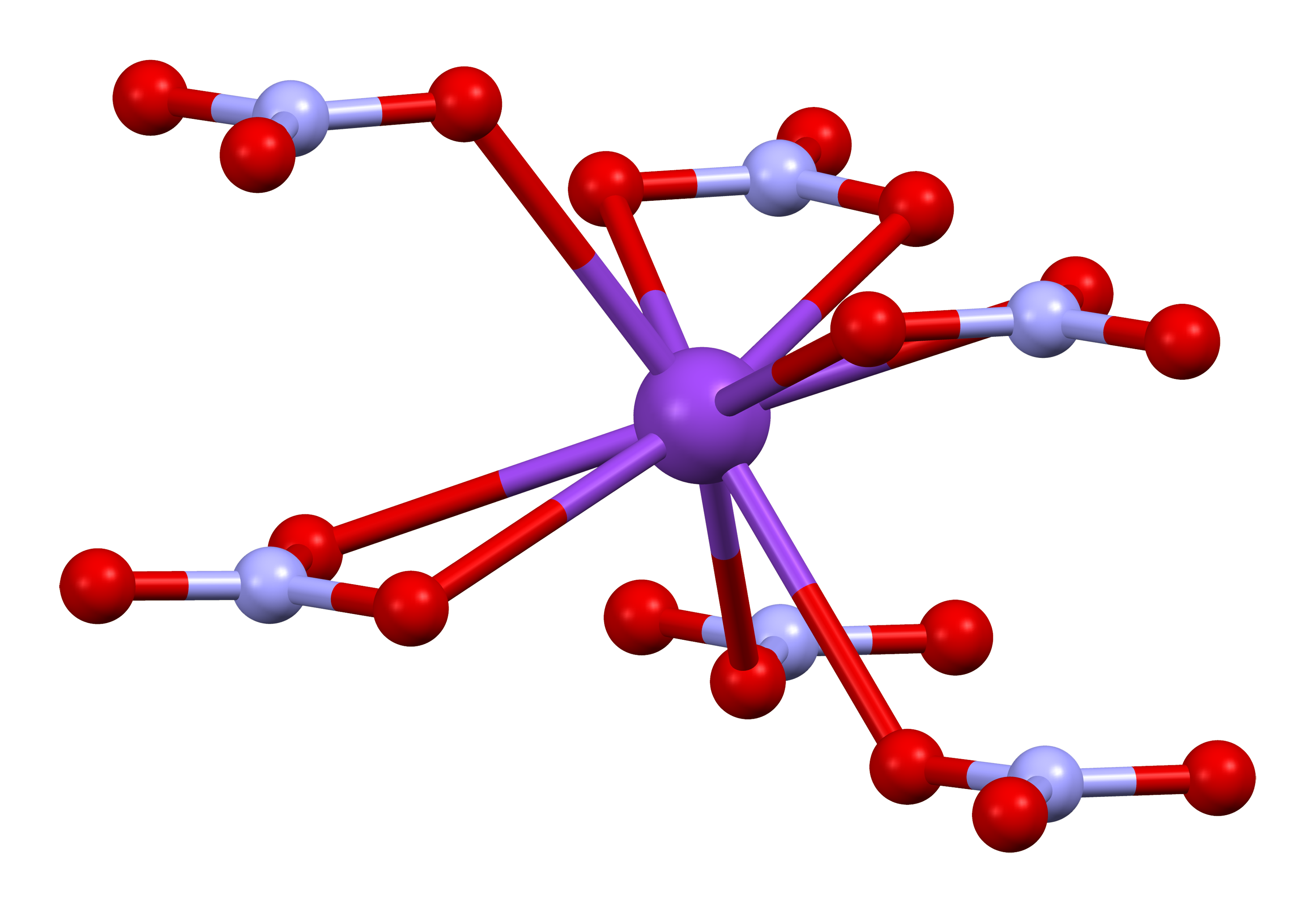
Nitrate and potassium coordinate geometries in the potassium nitrate crystal structure. Left: Nitrogen is at the center, surrounded by three oxygen atoms in red, and six potassium atoms in purple. Right: Potassium is at the center, surrounded by six nitrate molecules.

We will need data on each component of a reaction to calculate the energy required and to estimate kinetics. Hence, any reaction which consume or produce unstable molecules that there is no data for does not help our analysis. Alternatively one can find the so called transition state along the reaction coordinate of an elementary reaction through ab initio calculations. To narrow down the number of possible reactions paths, we can try to figure out all “reasonable” reactions which have “reasonable” components in them, where only bonds that can be supported by molecular structure are broken or formed. For example, the following breakdown can be made (not including any ionic intermediates)

$$ \begin{eqnarray} 2 KNO_3(s) + C(s) &\rightleftharpoons& K_2CO_3(s) + N_2O_3(g) \newline 2 KNO_3(s) + S(s) &\rightleftharpoons& K_2SO_4(s) + N_2O_2(g) \newline N_2 O_3(g) &\rightleftharpoons& N_2(g) + O_3(g) \newline N_2 O_3(g) &\rightleftharpoons& NO(g) + NO_2(g) \newline N_2 O_2(g) &\rightleftharpoons& N_2(g) + O_2(g) \newline % C + O_3 &\rightleftharpoons& CO_3 \newline % K_2^+ + CO_3^{2-} &\rightleftharpoons& K_2CO_3 \newline % 2KNO_3(s) &\rightleftharpoons& 2K^{+} + 2NO_3^{-} \newline % 2NO_3 &\rightleftharpoons& N_2 + 2O_3 (\text{not physical}) \newline % 2NO_3^- &\rightleftharpoons& N_2 + 2O_3 + 2e^- O_3(g) &\rightleftharpoons& O(g) + O_2(g) \newline C(s) + O_2(g) &\rightleftharpoons& CO_2(g) \newline CO(g) + O(g) &\rightleftharpoons& CO_2(g) \newline C(s) + O(g) &\rightleftharpoons& CO(g) \end{eqnarray} $$

It should be said that even the first reaction $2 KNO_3(s) + C(s) \rightleftharpoons K_2CO_3(s) + N_2O_3(g)$ can not be elementary since we are including the solid phase, which implies some form of structure of formation, either crystalline or amorphous. It actually does not make sense to talk about the solid phase for molecules in isolation; it is an aggregate phase which must incorporate at least two molecules (though even that can be doubtfully called solid phase). In fact, to properly model this one should include the position of the species in the particle. As a first classification, a molecule is either located in the bulk or at the surface of the particle, which in turn affects energies of reaction, which always happens at the surface. There are two interfaces one has to consider; one is the surface to external interface, the other is the surface to bulk. One way to deal with this is to make an instantaneous evaporation assumption, where all solid phase components are broken up into gas phase molecules by breaking all bulk bonds, and then one proceeds with the analysis of elementary gas phase reactions. This could be a good approximation for a highly exothermal reaction such as an explosion, but is unlikely to be accurate for other reactions. With that said, let us not dwelve 3 too deep into the rabbit whole in this post, but just note that this is still a very high level description of what is going on at the microchemistry level, and we will essentially treat each reaction as being in the gas phase, but still use energies tabulated for solids. Beware, I have no idea how accurate this approach is!

Let us visualize this graphically; let squares represent reactions, and circles represent chemical species. Reactants are colored orange, products green and intermediates purple. Note that both nitric oxide $NO$ and carbon monoxide $CO$ appears as “accidental product species” (as to be expected from a combustion reaction) marked in red. Clearly the original reaction specification is not complete, since it left these species out, unless reaction dynamics guarantees that they will not be formed at all.

%3 KNO3 KNO3 KNO3_C 2KNO3 + C KNO3->KNO3_C KNO3_S 2KNO3 + S KNO3->KNO3_S S S S->KNO3_S C C C->KNO3_C C_O2 C + O2 C->C_O2 C_O C + O C->C_O K2CO3 K2CO3 K2SO4 K2SO4 CO2 CO2 N2 N2 N2O3 N2O3 N2_O3 N2 + O3 N2O3->N2_O3 NO_NO2 NO + NO2 N2O3->NO_NO2 N2O2 N2O2 N2_O2 N2 + O2 N2O2->N2_O2 O O O->C_O O2 O2 O2->C_O2 O3 O3 O_O2 O + O2 O3->O_O2 NO NO CO CO KNO3_C->K2CO3 KNO3_C->N2O3 KNO3_S->K2SO4 KNO3_S->N2O2 C_O2->CO2 N2_O2->N2 N2_O2->O2 N2_O3->N2 N2_O3->O3 NO_NO2->O2 NO_NO2->NO O_O2->O O_O2->O2 C_O->CO

Incorporating $NO$ and $CO$ as products of the reaction gives the stoichiometric matrix

$$ \begin{pmatrix} 0 & 0 & 1 & -1 & 0 & -1 & 0 & -1 & 0 \newline 1 & 0 & 0 & -2 & -2 & 0 & 0 & 0 & 0 \newline 1 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & -1 \newline 3 & 0 & 0 & -3 & -4 & -2 & 0 & -1 & -1 \newline 0 & 1 & 0 & 0 & -1 & 0 & 0 & 0 & 0 \end{pmatrix} $$

which have a 4-dimensional nullspace, so finding a set of stoichiometric coefficients is even more difficult than before. The null space is (on row vector form)

$$ \begin{pmatrix}\vec{X} \newline \vec{Y} \newline \vec{Z} \newline \vec{W} \end{pmatrix}= \begin{pmatrix} 0 & -2 & 3 & 2 & -2 & 1 & 0 & 0 & 0 \newline 2 & 3 & -2 & -2 & 3 & 0 & 1 & 0 & 0 \newline 0 & -1 & 2 & 1 & 1 & 0 & 0 & 1 & 0 \newline 2 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 2 \end{pmatrix} $$

One valid solution including all species is $\vec{X} + \vec{Y} + \vec{Z} + \vec{W} = (6,1,6,2,1,2,2,2,2)$, or written on reaction form

$$ 6 KNO_3 + S + 6C \rightarrow 2K_2 CO_3 + K_2SO_4 + 2CO_2 + 2N_2 + 2CO + 2NO $$

which is very similar to the “minimal” reaction state $(a,b) = (4,3)$ identified earlier except for the coefficients of $CO_2$ and $N_2$ which are now allowed to decompose into $CO$ and $NO$.

Naturally, where one decides to draw the line and stop breaking down reactions into smaller subreactions is just a question of fidelity. For now, this amount of detail is a good start. How does this reaction diagram help us? Apart from identifying alternative byproducts, we can use it to simulate a reaction! To do that we need to annotate it with some more information to inform the simulation. The reaction rate constant $k$ for each node in the reaction graph is then given by an Arrhenius expression

$$ k = A \exp(-E_a / k_B T) $$

where $E_a$ is the activation energy (the energy barrier of surpassing the transition state), $k_B$ the Boltzmann constant, $T$ the temperature and $A$ the pre-activation which varies slowly with temperature and can usually be considered a constant. The forward rate and backward rate of a reaction on the form $mA + nB \leftrightharpoons pC + qD$ (the number of reactions occurring per unit time in each direction) are

$$\begin{align} \overset{\rightarrow}{r} &= \overset{\rightarrow}{k} [A]^m [B]^n \newline \overset{\leftarrow}{r} &= \overset{\leftarrow}{k} [C]^p [D]^q \end{align}$$

Annotating the reaction nodes of the reaction graph with the reaction rates then defines the reaction kinetics. To perform a simulation, the reaction rates has to be obtained either by experimentation or by ab-initio calculation of the activation energy. Initializing the system with known concentrations of each species, one can then simulate the progress of the total reaction by propagating the concentrations according to the rate in and out of reaction nodes by setting up a system of differential equations for the concentration / fugacity (partial pressure of a real gas) of each species. Let the net rate be the difference between the forward and backward rates: $r = \overset{\rightarrow}{r} - \overset{\leftarrow}{r}$. The rate of each participant in the reaction is then proportional to it’s stoichiometric coefficient

$$\begin{align} \frac{d[A]}{dt} &= - m r = m (\overset{\leftarrow}{k} [C]^p[D]^q - \overset{\rightarrow}{k} [A]^m[B]^n) \newline \frac{d[B]}{dt} &= - n r = n (\overset{\leftarrow}{k} [C]^p[D]^q - \overset{\rightarrow}{k} [A]^m[B]^n) \newline \frac{d[C]}{dt} &= \nm p r = p (\overset{\rightarrow}{k} [A]^m[B]^n - \overset{\leftarrow}{k} [C]^p[D]^q) \newline \frac{d[D]}{dt} &= \nm q r = q (\overset{\rightarrow}{k} [A]^m[B]^n - \overset{\leftarrow}{k} [C]^p[D]^q) \newline \end{align}$$

By using these rate expressions in a simulation and running until equilibrium is reached, the stoichiometric coefficients can be obtained by looking at the relative concentrations of the product and reactant species, which in general does not yield integral coefficients! Now to further complicate things, this particular reaction is violent with time varying temperature and pressure, so the “rate constants” are actually “rate variables”. This is where I picked up a book on chemical kinetics and decided to not dive down the next level of the rabbit hole… but to release this peacock of an idea into the wild!

Appendix

Python script used to compute the stoichiometric matrices

import numpy as np
from sympy import Matrix, lcm

def canonical(A):
    b = lcm([a.q for a in A])
    return A * b

def pretty(N):
    return np.array2string(np.array(canonical(N), dtype=int).squeeze())

print('C2H6 + O2 -> 4CO2 + H2O')
C = Matrix([
    [2, 0, -1,  0],
    [6, 0,  0, -2],
    [0, 2, -2, -1]
])
N = C.nullspace()
print(pretty(N[0]))

print('KNO3 + S + C -> K2CO3 + K2SO4 + CO2 + N2')
C = Matrix([
    [0, 0, 1, -1,  0, -1,  0],
    [1, 0, 0, -2, -2,  0,  0],
    [1, 0, 0,  0,  0,  0, -2],
    [3, 0, 0, -3, -4, -2,  0],
    [0, 1, 0,  0, -1,  0,  0]
])
N = C.nullspace()
print('#1   :', pretty(N[0]))
print('   #2:', pretty(N[1]))
print('#1+#2:', pretty(N[0] + N[1]))

print('KNO3 + S + C -> K2CO3 + K2SO4 + CO2 + N2 + CO + NO')
C = Matrix([
    [0, 0, 1, -1,  0, -1,  0, -1,  0],
    [1, 0, 0, -2, -2,  0,  0,  0,  0],
    [1, 0, 0,  0,  0,  0, -2,  0, -1],
    [3, 0, 0, -3, -4, -2,  0, -1, -1],
    [0, 1, 0,  0, -1,  0,  0,  0,  0]
])
N = C.nullspace()
print(len(N))
print('#1         :', pretty(N[0]))
print('   #2      :', pretty(N[1]))
print('      #3   :', pretty(N[2]))
print('         #4:', pretty(N[3]))
print('#1+#2+#3+#4:', pretty(N[0] + N[1] + N[2] + N[3]))

  1. Principles of Chemistry I, Chapter 3, last slide ↩

  2. https://www.sympy.org/en/index.html ↩

  3. This is hilarious, when proofreading this post my spellchecker complained about this word. I have used a word which doesn’t exist my whole life, and it seems that many others have too! See Reddit thread here (not sure if the misspelled title is a pun or not, LOL!): Does the world dwelve exist? ↩